Решить онлайн дифференциальные уравнения - просто! Искусственный интеллект постоянно развивавется. Нашим специалистам удалось научить его решать различные математические задачи. Например, стали доступны такие раздеолы, как решение онлайн дифференциальных уравнений или производная функции онлайн.
На нашем сайте вы можете решить любое дифференциальное уравнение используя Калькулятор за пару секунд. Пользоваться калькулятором просто. Начальные условия вводите как обычные условия. Порядок не важен. Чтобы ввести условие, нажмите «+условие»
Например:
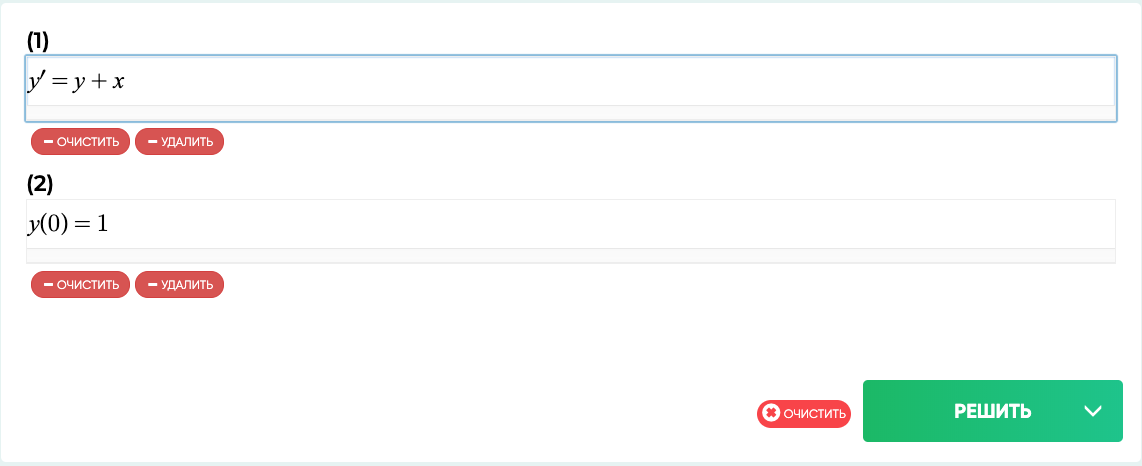
Условие 1: y'=y+x
Условие 2: y(0)=1
Нажав кнопку Решить вы получите подробное решение дифференциальных уравнений.
Дифференциальное уравнение (ДУ) – это уравнение с производными функции или самой функцией, независимой переменной и параметрами. Чтобы научиться решать дифференциальное уравнение, нужно сначала разобраться с условными обозначениями. Производная функции обозначается символически “штрихом”. Производная функции второго порядка отображается соответственно двумя “штрихами” и так далее.
Порядок дифференциального уравнения – это порядок старшей производной в уравнении.
Решение дифференциального уравнения не будет таким же, как решение обыкновенного уравнения. Решением дифференциального уравнения будет функция или семейство функций. Производные могут входить в функцию в любом порядке и сами производные могут быть любого порядка. Производные, функции, независимые переменные и параметры могут входить в ДУ в различных комбинациях или же могут вовсе отсутствовать. Однако в уравнение должна входить хотя бы одна производная, иначе оно бы не будет дифференциальным. Дифференциальным уравнением является не любое уравнение, содержащее производные неизвестной функции. К примеру, f'(x)=f(f(x)) не является дифференциальным уравнением, а просто обозначает производную от определённой функции.
При решении дифференциальных уравнений, в отличие от алгебраических уравнений, ищется не число или несколько чисел, а функция или семейство функций. Алгебраический смысл решения таковой: если вместо функций и производных всех порядков, подставить любую функцию из семейства её решений, то получится верное равенство.
ДУ выше первого порядка возможно преобразовать в систему уравнений первого порядка, где число уравнений равняется порядку исходного дифференциального уравнения. Таким образом дифференциальное уравнение второго порядка преобразуется в систему функций, состоящую из двух уравнений.
При решении такой задача, как дифференциальные уравнения важно помнить, что его решением будет именно семейство функций, так как если брать производную от константы, то она будет равняться нулю. А так как производная от константы равняется нулю, то в исходной функции может быть такое определённое решение данного дифференциального уравнения. Не все калькуляторы позволяют решить дифференциальные уравнения онлайн, а только самые “умные”. Ещё несколько лет назад решить дифференциальное уравнение с помощью калькулятора было невозможным.
Система дифференциальных уравнений, линейные дифференциальные уравнения или другое дифференциальное уравнение любой сложности будет решено нашим бесплатным решателем за считанные секунды. Все, что вам необходимо сделать - это просто ввести данные уравнения в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить дифференциальное уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в онлайн чате на странице Калькулятора или в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Так же читайте нашу статью "Решить систему уравнений методом сложения онлайн решателем"
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!