Тригонометрия

Онлайн решение тригонометрических уравнений

На нашем сайте вы можете решить любое тригонометрическое уравнение используя Калькулятор за пару секунд. Решать уравнения тригонометрические с помощью калькулятора просто. Чтобы ввести условие, нажмите «+условие»

Например:

Условие: sin2x+3x=2

Нажав кнопку Решить вы получите подробное решение тригонометрических уравнений.

Тригонометрия это просто если вы знаете формулы приведения в тригонометрии.

Тригонометрия 10 класс

Для начала нужно обязательно запомнить основные формулы.

Тригонометрия таблица

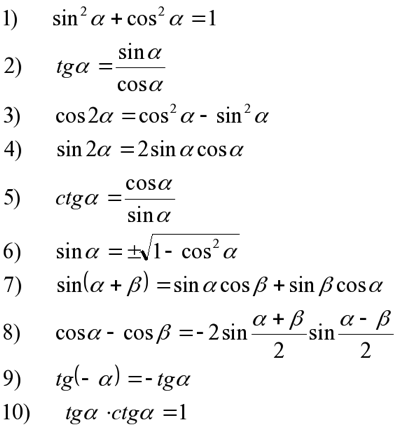
Тригонометрия приведение

Главной задачей при решении тригонометрических уравнений является его преобразование до более простого уравнения основного вида, которое решаются стандартными методами. Для решения данного рода уравнений можно использовать один из семи методов:

- алгебраический;

- разложения на множители;

- преобразования к одному уравнению;

- перехода к половинному углу;

- вспомогательного угла;

- преобразования произведения в сумму;

- подстановки.

Так же читайте нашу статью "Решить систему тригонометрических уравнений онлайн решателем"

Выбор метода определяется исходя из самого уравнения. Одно уравнение можно решить несколькоми способами, однако при правильном выборе метода вы решите его за меньшее количество математических операций.

Допустим, нам дано уравнение такого вида:

\[\sin x + \cos x = 1\]

Чтобы решить данное уравнение необходимо воспользоватся 2м методом и выполнить перенос всех членов влево:

\[\sin x +\ cos x - 1 = 0\]

Теперь преобразуем и разложим на множители левую часть уравнения:

\[\sin x -2 sin^2(\frac {x}{2})=0\]

\[2\sin(\frac {x}{2})\cdot\cos(\frac {x}{2})-2\sin^2(\frac {x}{2})=0\]

\[2\sin(\frac {x}{2})\cdot[\cos(\frac {x}{2}) - \sin(\frac {x}{2})]=0\]

1)

\[\sin (\frac {x}{2})=0\]

\[\frac{x}{2}\pi k\]

\[x_1=2\pi k\]

2)

\[\cos(\frac {x}{2})-\sin(\frac {x}{2})=0\]

\[\tan\frac {x}{2}=1\]

\[\frac {x}{2}=\arctan 1 +\pi n\]

\[\frac {x}{2} = \frac {\pi}{4}+\pi n\]

\[x_2 = \frac {\pi}{2}2\pi n\]

Где и как решать тригонометрические уравнения онлайн?

Решить уравнение вы можете на нашем сайте. Бесплатный решатель позволит решить тригонометрические уравнения с решениями любой сложности за считанные секунды онлайн. Тригонометрия егэ больше не проблема. Все, что вам необходимо сделать - это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Используя наш калькулятор тригонометрический, вы всегда сможете сказать, что тригонометрия класс!