And astronomers, who determine the orbits of celestial bodies, and architects, who calculate the strength of the designed buildings, use the same powerful tool. This is mathematics - one of the most ancient sciences created by people. It is interesting that in itself it is not tied to the surrounding reality in any way and deals with purely abstract objects. Why, then, in order to calculate algebra in physics, you inevitably have to resort to mathematics? An unambiguous answer to this like would a simple question not exist today.
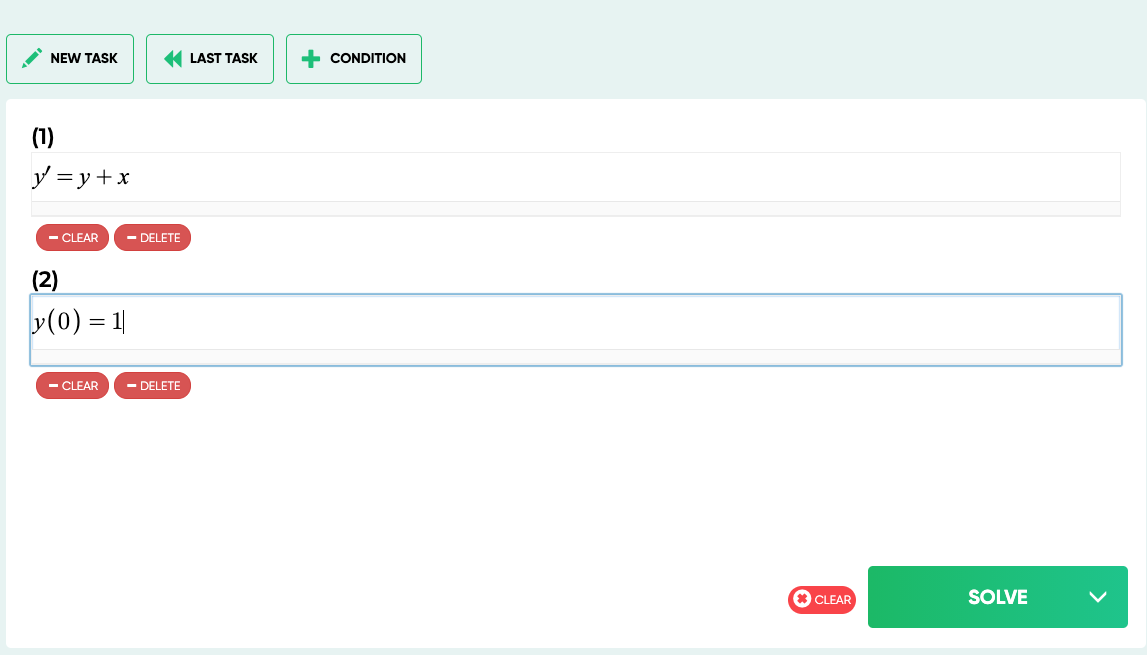
The emergence of the so-called elementary mathematics began with simple arithmetic, which was required at the lowest, everyday level. The quantitative ratios were determined in this case between quite real physical objects. Some scientists believe that all mathematics as a whole was formed on the basis of observation of the surrounding world.
In accordance with this hypothesis, the creation and development of algebra and geometry became possible thanks to formed on the "natural" basis of the way of thinking and spatial imagination. In this way, real physical objects simply cannot but correspond to one or another mathematical model, you just need to find such a match.
The "observational" hypothesis is supported, in particular, by the fact that Newton, when creating a differential calculus pursued the goal of solving problems in mechanics. Thus, classical physics and mathematical analyzes were born simultaneously and in interaction, which can be called a very typical example.
There is another answer to the question of the relationship between the two greatest sciences. Supporters of this approach, it is believed that mathematical objects have always existed and will remain forever, regardless of whether scientists will discover them. At the same time, the surrounding reality is a kind of subset, a small a part that is remarkable only for being in direct contact with researchers. With this point of view, physics is only a small part of mathematics, and it is not surprising that in both sciences, the same general rules apply, math solver is carried out in the same way.
The fact that over time, more and more correspondences are sought between real phenomena and earlier purely abstract models, to some extent confirms the second hypothesis. In particular, the set differential equations even in the 19th century looked like purely abstract constructions, and in the next century it turned out that they describe previously unknown physical objects. And if this theory is correct, then objects with extremely unusual properties can be found in the Universe - after all, mathematics is infinite diverse, and the constructions in it are limited only by the imagination of scientists.
Our artificial intelligence solves complex math problems in seconds.
We will solve your exam, homework, olympiad problems with detailed steps. You will need just to copy the solution.