Mathematical expressions are found for children and adults. A common expression is the factorial integer, which is denoted as n! and is a product from one to n. It is applicable only to non-negative values greater than zero, often used to solve a math problem . Mathematicians have adopted the definition "0!", Equal to one.
The concept of factorial appeared in the 19th century, since that time tables have been created that describe the final the values of the product of numbers for each example "n!" up to "25!" Data can be used in ready form when working without wasting time on recalculating them.
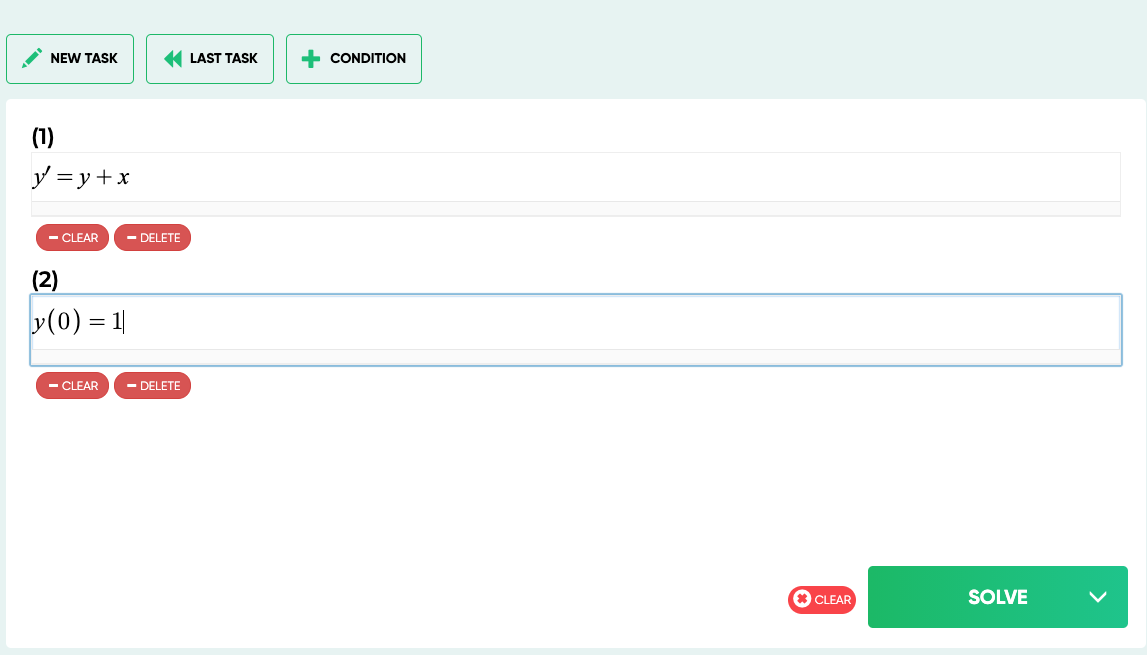
Formulas that simplify the solution
The use of factorial has found wide application in combinatorics: combinations, permutation, and placements. By calculating algebra and equations, you need to find unknown value. To simplify the calculation, the following rules apply:
- "2n !!" is equal to the product of all even numbers 2, 4, 6, 8 and others;
- "(2n + 1) !!" applies to all digits like 1, 3, 5 and the like;
- there is an equality “2n !! * (2n + 1) !! = (2n + 1)!” or “2n !! * (2n-1) !! = 2n!”.
If there are factorials in the example with several terms of the equation, then the smaller one is highlighted and out of parentheses. This simplifies the calculation as it requires a simpler product the remaining parameters and the total value. In the presence of fractions, in the numerator and denominator of which are given factorials, it is possible to change them by finding the same part. It is placed outside the brackets and then is shortened.
There is a method for calculating functions from the previous value. The calculation is shown in an example: 4! = 4 * 3! or 4 * (3 * 2 * 1). In mathematics of high school and primary courses of higher educational institutions, Gamma function and Newton binomial.
To calculate large values and solve complex equations with a factorial, it is possible to use software, as manual work with them would be too time consuming, and online calculators give an error. There are special applications and scripts that calculate the total from specified parameters.